Naprej: na klancu Navzgor: statika Nazaj: statika Kazalo
Torej:
![]() = -
= - ![]()
Velikosti obeh sil sta enaki:
F = Fg = mg = 100kg . 10m/s2 = 1000N
Torej:
![]() = -
= - ![]()
Velikosti obeh sil sta enaki:
F = Fg = mg = 2kg . 10m/s2 = 20N
in to je to ;)
m1 = 0.3kg
x1 = 1.5cm = 0.015m
m2 = 0.5kg
F = k . x0
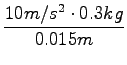
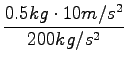
![]() +
+ ![]() =
= ![]()
Hmm to se fazani učijo...škoda da ne znajo kotnih funkcij.
No fazani mate tm eno lepo slikco.. pa se znajdte.
F = ![]() =
= ![]() = 1, 41N
= 1, 41N
pri kotu
![]() = 60o, kajti tedaj ležijo sile na stranicah enakostraničnega trikotnika
= 60o, kajti tedaj ležijo sile na stranicah enakostraničnega trikotnika
Fa = 20N + 15N = 35N
Fb = 20N - 15N = 5N
Fc = ![]() = 25N
= 25N
Fa = 28N
Fb = 4N
Fc = 20N
2.: vsota zunanjih sil na opazovano telo je produktu med maso telesa in njegovim pospeškom.
3.reakcija: Če 1. telo deluje na 2. telo z neko silo, potem tudi 2. telo deluje na 1. telo z nasprotno enako silo.
Zaviralne sile: LEPENJE, TRENJE, UPOR.
TRENJE: deluje med nekim telesom in neko stvarjo (tla, drugo telo...).
Telo se pri trenju GIBLJE.
LEPENJE: deluje med nekim telesom in neko stvarjo (tla, drugo telo...).
Telo se pri lepenju NE GIBLJE.
UPOR: (npr.zraka):ko neko telo npr. pada s stolpnice ima manjši pospešek od 9,81 m/s2, ker ga upor zraka zaustavlja. Tako telo pade na tla z manjšo hitrostjo, kot pa bi pri padu brez upora zraka (prosti pad).
NE POZABI NAPISATI NEWTONOVE ZAKONE ŠE S SIMBOLI!!!!!
Fkroglice = 4N
RAZBEREMO Z SLIKE 12:
Fsilomera = ![]() .
. ![]() = 2N . 1, 41 = 2, 8N
= 2N . 1, 41 = 2, 8N
če naj silomera pokažeta 2 krat večjo silo, potem mora vsak kazati 8N, ne pa 4N in zato trikotnik ni več enakostranični - je pa naloga težja;)
velja:
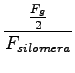
ker je: Fsilomera = 2Fg
sledi:
in
![]() = 75, 6o
= 75, 6o
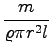 = 107, 3m
= 107, 3m
gostota H2O je 1kg/dm3
a)
b)
c)
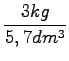 = 0, 53kg/dm3
= 0, 53kg/dm3
sila vzgona:
Fv = ![]() gV = 31, 4N
gV = 31, 4N
sila, s katero je napeta žica: F = Fv - Fg = 11, 4N
del žoge pod vodo:
![]() =
= ![]() =
= ![]() = 0, 635
= 0, 635
Premer posode je d = 2, 257cm in zato je presek valjaste posode
S = ![]() r2 = 4cm2. Število kovancev v posodi je označil z N, višino potopljenega dela posode pa s h. Izmerjene podatke je zapisal v tabelo.
r2 = 4cm2. Število kovancev v posodi je označil z N, višino potopljenega dela posode pa s h. Izmerjene podatke je zapisal v tabelo.
| N | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| h [cm] | 9,4 | 10,3 | 12 | 13,49 | 15 | 16,9 | 17,6 |
Nariši graf prostornine potopljenega dela posode v odvisnosti od števila kovancev! Koliko je masa enega kovanca? Koliko je masa valjaste posode?
h1 ![]() 1, 5cm,
V1
1, 5cm,
V1 ![]() 6cm3,
m1
6cm3,
m1 ![]() 6g,
mß
6g,
mß ![]() 12g
12g
Premer posode je d = 2, 257cm in zato je presek valjaste posode
S = ![]() r2 = 4cm2. Število kovancev v posodi je označil z N, višino potopljenega dela posode pa s h. Izmerjene podatke je zapisal v tabelo.
r2 = 4cm2. Število kovancev v posodi je označil z N, višino potopljenega dela posode pa s h. Izmerjene podatke je zapisal v tabelo.
| N | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| h [cm] | 8,2 | 10,05 | 11 | 12,25 | 13,5 | 14,45 | 16,3 |
Nariši graf prostornine potopljenega dela posode v odvisnosti od števila kovancev! Koliko je masa enega kovanca? Koliko je masa valjaste posode?
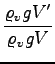 =
= 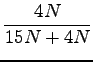 = 0, 21 = 21%
= 0, 21 = 21%
po varianti a) izračunamo koeficient prožnosti
k = ![]() (= 2/4N/cm = 0, 286N/cm); no saj nam računa ni treba končati!
(= 2/4N/cm = 0, 286N/cm); no saj nam računa ni treba končati!
nato silo vzgona:
Fv = k(x1 - x2) = ![]() (x1 - x2) (=
(x1 - x2) (= ![]() )
)
nato pa iz razmerja med težo in vzgonom izračunamo gostoto uteži:
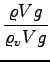 =
= 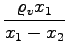 = 3, 5
= 3, 5
po varianti b) ravno tako izračunamo koeficent prožnosti k ter silo vzgona
Fv = k(x1 - x2) = ![]() Vg
Vg
nadaljujemo malo drugače:
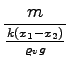 =
= 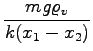 =
= 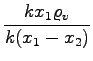 =
= 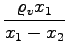 = 3, 5
= 3, 5in zanimivo - rezultat sploh ni odvisen od koeficienta prožnosti vzmeti!
Fv = 64mN
Fg = 64mN
Fg' = 448mN
![]() =
= ![]()
![]() = 0, 583kg/dm3
= 0, 583kg/dm3
Fv = ![]() gV =
gV = ![]() ga2h = 10, 08N
ga2h = 10, 08N
Fg = 10, 08N
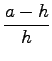 = Fv
= Fv
me 2007-11-05