Naprej: dinamika Navzgor: statika Nazaj: na klancu Kazalo
Izrazimo recimo razdaljo r1 in izračunamo:
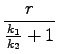 =
= 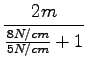 = 0, 77m = 77cm
= 0, 77m = 77cm
Če upoštevamo še maso palice, potem imamo težave, saj se vzmeti že na začetku raztegneta. Vsekakor je rezultat odvisen od mase palice!
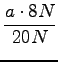 =
= 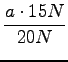 =
=
e.g:. Na sliki 15 smo se odločili, da bomo potisnili kvader v točki levo zgoraj in sicer tako, da se bo zavrtel okoli roba. In še vedno imamo precej možnosti, da si izberemo smer delovanja sile. Od obojega je odvisna velikost sile. V vsakem primeru moramo delovati s tolikšno silo, da bo njen navor vsaj tolikšen, kot je navor teže kvadra: M ![]() Mg!
Mg!
Če si izberemo smer navpično navzgor (sila F na sliki 15), kakor bi dvigovali kvader, če bi stal na največji ploskvi, potem lahko računamo takole:
Ker je prostornina kvadra
V = abc = 200cm3 in masa kvadra
m = ![]() V = 2, 04kg, je sila F = 10, 2N.
V = 2, 04kg, je sila F = 10, 2N.
Če si izberemo smer sile F1, ki je vzporedna s podlago:
Če si izberemo smer sile F2, ki je pravokotna na diagonalo:
To je le nekaj primerov, kako lahko takšno nalogo rešimo.
S tem pa ni konec težav in zapletov! Hitro ugotovimo, da se bo sila s katero moramo delovati na kvader zmanjševala, ko ga bomo prevračali. Ostane še vprašanje, ali je trenje dovolj veliko, da kvader ne bo zdrsnil ...
Na začetku se mi je zdelo, da je takšna naloga, pri kateri ni ene same rešitve, nekako manjvredna. Med reševanjem sem mnenje spremenil. Naloga pušča dovolj možnosti, nekatere rešitve so enostavne, kot te, ki sem jih zapisal, druge bolj zapletene.
ravnovesje sil:
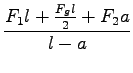 = 670N
= 670N
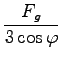 = 1154N
= 1154N
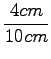 = 0, 4
= 0, 4
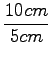 = 2
= 2
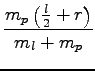 = 12, 7cm
= 12, 7cm
me 2007-11-05