Naprej: na klancu Navzgor: dinamika Nazaj: dinamika Kazalo
na primer takole:
a) Po 2.Newtonovem zakonu je pospešek razmerje med vsoto vseh zunanjih sil in maso opazovanega telesa:
pospešek je različen od 0, zato je gibanje premo enakomerno pospešeno:
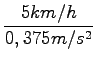 =
= 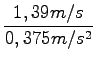 = 3, 7s
= 3, 7s
b) Če upoštevamo še trenje
se spremeni vsota vseh zunanjih sil na voz-potem je vsota vseh zunanjih sil:
F = Fb - F(tr) = 30N - 24N = 6N
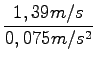 = 18, 5s
= 18, 5s
c) NARIŠEMO SLIKO (glej glej slika manjka!)
Razberemo: Fg = 800N, Fb = 30N,
Fp = 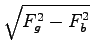 = 799, 4N
= 799, 4N ![]() 800N
800N
branjevka lahko potiska voz s stalno hitrostjo v klanec tedaj, ko je Fb tako velika kot vektorska vsota Fg in Fp;
ali zapisano malo drugače:
![]() +
+ ![]() +
+ ![]() = 0
= 0
sile lahko narišemo v pravokotni trikotnik!
strmina klanca je enaka razmerju sile s katero branjevka potiska voz in silo podlage:
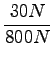 = 0, 0375
= 0, 0375
to pomeni, da se na 100m vodoravne razdalje lahko klanec dvigne za 3.75m
![\includegraphics[width=150pt]{sile-navzgor-1}](img116.png)
![\includegraphics[width=150pt]{sile-vodoravni}](img117.png)
vsota zunanjih sil na padalca: F = ma = - 350N
sila padala na padalca: Fp = Fg - F = 1050N, če smeri sil upoštevamo s predznaki, ali Fp = Fg + | F| = 1050N, če računamo samo z velikostmi sil.
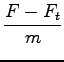 = 0, 2m/s2
= 0, 2m/s2
t = ![]() = 25s
= 25s
s = ![]() = 62, 5m
= 62, 5m
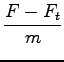 = 0, 1m/s2
= 0, 1m/s2
t = ![]() = 30s
= 30s
s = ![]() = 45m
= 45m
a = ![]() =
= ![]() m/s2 = 1, 11m/s2
m/s2 = 1, 11m/s2
in tako je čas:
t = ![]() = 1, 9s
= 1, 9s
drugi Newtonov zakon, če upoštevamo silo trenja
Ft = ![]() Fp, kjer je
Fp, kjer je ![]() koeficient trenja:
koeficient trenja:
drugi Newtonov zakon, če ne upoštevamo trenja:
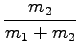
Podatki niso pravi - kaj takega se ne bi moglo zgoditi! Pri isti poti s = 32m bi moral biti čas vsaj:
drugi Newtonov zakon, če ne upoštevamo trenja:
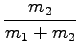 =
=
me 2007-11-05