Naprej: pri kroženju Navzgor: dinamika Nazaj: sile Kazalo
pospešek:
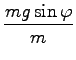 = g sin
= g sin
drugi Newtonov zakon, če upoštevamo silo trenja
Ft = ![]() Fp, kjer je
Fp, kjer je ![]() koeficient trenja:
koeficient trenja:
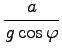 = 0, 43
= 0, 43
Sedaj se spomnim prvega Newtonovega zakona: vsota zunanjih sil na kolesarja je enaka masi kolesarja pomnoženi z njegovim pospeškom. Ker pravokotno komponento teže F![]() uravnovesi podlaga, je zato vsota zunanjih sil:
F = F || - Ft = 32, 5N. Pospešek kolesarja, ko se spusti po klancu:
uravnovesi podlaga, je zato vsota zunanjih sil:
F = F || - Ft = 32, 5N. Pospešek kolesarja, ko se spusti po klancu:
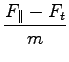 = 1, 44m/s2
= 1, 44m/s2
Ko enkrat poznam pospešek, lahko s pomočjo enačbe, ki povezuje pospešek, pot in hitrost izračunam dolžino klanca.
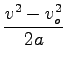 = 69, 4m
= 69, 4m
V drugem delu naloge se kolesar pelje po ravnini. Ker je vsota zunanjih sil naj enaka trenju, se mu hitrost zmanjšuje. Računam podobno kot prej, le da moram upoštevati, da je sedaj sila trenja malenkost večja kot prej, saj je sedaj sila, ki je pravokotna na podlago enaka teži. Trenje na vodoravni podlagi je: Ft = ktFg = 33N.
Pospešek (pojemek):
a = ![]() = - 0, 3m/s2
= - 0, 3m/s2
pot, ki jo prepelje:
s = ![]() =
= ![]() = 41, 7m
= 41, 7m
me 2007-11-05