Naprej: nihajni krog Navzgor: nihanje Nazaj: nihanje Kazalo
![\includegraphics[width=180pt]{hitrost.png.eps}](img225.png) [graf odmika v odvisnosti od časa]
[graf odmika v odvisnosti od časa]
![\includegraphics[width=180pt]{odmik.png.eps}](img226.png) [graf pospeška v odvisnosti od časa]
[graf pospeška v odvisnosti od časa]
![\includegraphics[width=180pt]{pospesek.png.eps}](img227.png) |
vem:
v(t) = v0 . cos(![]() . t)
. t)
![]() -kotna hitrost-kotna frekvenca
-kotna hitrost-kotna frekvenca
iz enačbe razberemo, da je
![]() = 1, 5s-1 in največja hitrost v0 = 5cm/s
= 1, 5s-1 in največja hitrost v0 = 5cm/s
izračunamo še nihajni čas:
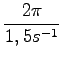 = 4, 2s
= 4, 2s
torej graf v(t) lahko narišeš brez problema. graf cosinusa je v y-osi razpotegnjen do 5, v x-osi pa raztegnjen na 1.5. Torej so hribčki in dolince malo bolj skupaj.
graf
x(t) = x0 . sin(![]() . t)
. t)
največja hitrost je:
v0 = ![]() . x0, kjer je x0-amplituda
. x0, kjer je x0-amplituda
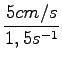 = 3, 33cm
= 3, 33cm
pospešek:
a(t) = - ![]() . x(t) = -
. x(t) = - ![]() . x0 . sin(
. x0 . sin(![]() . t)
. t)
t0 = 2 . 0.25s = 0.5s - je to jasno?
ne? to je zato, ker je nihajni čas čas, ki ga porabi nihalo da pride iz začetne lege zopet v to lego. :)
![]() - frekvenca
- frekvenca
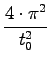 =
= = > l - dolžina nihala
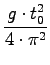 =
= 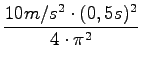 = 0, 0633m = 6, 3cm
= 0, 0633m = 6, 3cm
:)
![]() = 10Hz
= 10Hz
a = 5cm
![]() ...kotnafrekvenca =
...kotnafrekvenca = ![]()
![]() = 10Hz pomeni da v
to = 0.1s naredi nihalo en nihaj
= 10Hz pomeni da v
to = 0.1s naredi nihalo en nihaj
Torej je odmik on RL po 4s ====== 0 m.
največja hitrost je v RL
vo = xo . ![]()
vo = xo . ![]()
vo = 0.05m . ![]()
vo = 3.1m/s
največji pospešek pa je v SL
ao = xo . ![]()
ao = xo . ![]()
![]()
![]()
ao = 0.05m . ![]()
![]() )
)![]()
ao = 197m/s2
v0 = ![]() . x0
. x0
ker je krožna hitrost ali krožna frekvenca:
![]() =
= ![]()
je tako hitrost:
vo = ![]() . xo ,kjer je xo = 30cm amplituda nihanja, krožna frekvenca
. xo ,kjer je xo = 30cm amplituda nihanja, krožna frekvenca
![]() =
= ![]()
zato lahko zapišemo, da je hitrost:
odtod izračunamo nihajni čas nihala:
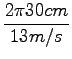 = 0.145s
= 0.145s
lahko izrazimo dolžino
Torej je sekundno nihalo dolgo četrt metra.
To lahko opazimo na starih stenskih urah, ki imajo dolžino nihala ravno 25cm .
to = 0.5s
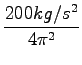
m = 1kg ...ker so podatki na eno mesto...drgač pride na kalkulator 1.2665kg
the TOK MISLI:
zdej grem pa spat.. jutr bom še ene par naredu...tko da se prpravte da me bote popravl.. lol
smešn.. a kdo to bere ob petkih zvečer...damn mi je dolgcajt
kpr = 15N/m = 15kg/s2
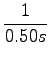 = 2Hz
= 2Hz
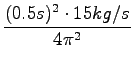 = 0.095kg = 95g
= 0.095kg = 95g
![]() ...krožna frekvenca
...krožna frekvenca
Ker vemo da se gibalna količina ohranja:
Klada miruje torej je njena hitrost enaka 0.
vk = vo
vo = xo . ![]()
vo = 0.24m . 2.2s-1
vo = 0.53m/s
ker se gibalna količna ohranja: Gz = Gk ali G1 + G2 = Gk je:
0 + v2 . m2 = vk(m1 + m2)
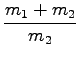 = 0.53m/s
= 0.53m/s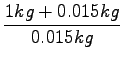 = 35m/s
= 35m/s
To nihanje si moramo predstavljati, kot da je sestavljeno iz dveh nihanj z različnima dolžinama vrvice.
Nihajni čas: l1 = 5m, s = 3m,
![]() l2 = l1 - s = 2m
l2 = l1 - s = 2m
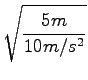 =
=
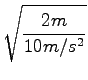 =
=
nihajni čas je t0 = 3s:
t0 = t1/2 + t2/2
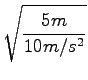
Torej mora biti čep 5m - 0, 614m = 4, 39m pod pritrdiščem.
Rezultat je povsem verjeten, saj če je čep višje je nihajni čas daljši, če je pa nižje je krajši.
Za 5s se ponovi enačba. Vendar, če ugotovite, da je maksimalni čas nihala lahko le 4.4s. Torej za 5s ne gre. Nekdo se je pošalil iz vas...hecno
...drugače je lažje zračunat.. po moje če ne izraziš x ampak takoj vstaviš not številke.. samo to je kao prou...
ali
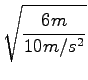 = 4, 9s
= 4, 9s
najprej določimo amplitudo (glej sliko 33!): x02 - c2 = l2 - b2
x0 = ![]()
x0 = ![]()
x0 = 1, 5m
nato največjo hitrost:
v0 = ![]() . x0
. x0
v0 = ![]() . x0
. x0
v0 = ![]() . 1.5m
. 1.5m
v0 = 1.9m/s
skupna energija:
W = W(p(max)) = m . g . h
Wp = 4kg . 10m/s2 . 0.2m
Wp = 8J
in še kinetična v izbrani legi:
Wk = W - Wp
Wk = W - m . g . h
Wk = 8J - 4kg . 10m/s2 . 0.05m
Wk = 6J
W2 = 100mJ = 0, 1J
Ker poznamo enačbo za dušeno nihanje
Wk = ![]()
2J = m . v02/2 ...Masa uteži ostaja enaka...torej jo lahko črtamo. Ob črtanju mase moramo upoštevati, da se tudi enote krajšajo.Lahko jo tudi pustite, saj se v naslednji enačbi krajša.
v0 = 2m/s
Potem pa izračunamo še za energijo po 25s. In uporabimo Wk = W2
Za nihajni čas, ki se ne spreminja ne glede na amplitudo odmika, pogojen je namreč le s težnim pospeškom in dolžino nihala(pri nitnem nihalu), vzamemo t0 = 5s.
W2 = ![]()
0, 05s = e-![]() 50s ...Za tiste , ki jim logaritmi niso povsem jasni.
50s ...Za tiste , ki jim logaritmi niso povsem jasni.
0, 05s = e![]() . e-50
. e-50
ln e![]() =
= ![]()
![]() = 47
= 47
Končno rezultat.
Pol je treba pa še narisat. Če slučajno bere to kdo, ki ima Derive ali kak programček za risanje grafov, bi ga prosil, da doda graf. Hvala!!!
ali pa:
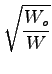
tako je
![]() = 0, 06s-1
= 0, 06s-1
khm...kateri je pravi?
![\includegraphics[width=180pt]{s_duseno-energija.png.eps}](img229.png)
|
fizikalno ozadje:
če je hitrost na začetku največja, se v odvisnosti od časa spreminja takole:
pri tem je vo začetna hitrost, ![]() koeficient dušenja;
koeficient dušenja;
prvi del enačbe
v = voe-![]() t nam pove, kako se spreminja amplituda hitrosti, drugi del
cos(
t nam pove, kako se spreminja amplituda hitrosti, drugi del
cos(![]() t) pa govori o nihanju!
t) pa govori o nihanju!
potem spreminjanje kinetične energije opiše enačba:
kjer je Wo začetna kinetična energija, člen
e-2![]() t opisuje eksponentno manjšanje skupne (in s tem tudi največje kinetične) energije, člen
cos2(
t opisuje eksponentno manjšanje skupne (in s tem tudi največje kinetične) energije, člen
cos2(![]() t) pa osciliranje trenutne kinetične energije.
t) pa osciliranje trenutne kinetične energije.
sedaj pa k reševanju
največja kinetična energija eksponentno pada:
W(ko) = Woe-2![]() t
t
torej je:
![]() = e-2
= e-2![]() t
t
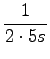 ln
ln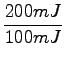 = 0, 0693s-1
= 0, 0693s-1
narišimo grafa
Wko = Woe-2![]() t in
Wk = Woe-2
t in
Wk = Woe-2![]() tcos2(
tcos2(![]() t)
t)
Wk = W1 = 200mJ = 0, 2J S tem je mišljena maksimalna Wk, ko ima nihalo največjo hitrost.
W2 = 100mJ = 0, 1J
Ker poznamo enačbo za dušeno nihanje
v = v0 . e-![]() tcos(
tcos(![]() . t), lahko rečemo tudi:
v0 = v0 . e-
. t), lahko rečemo tudi:
v0 = v0 . e-![]() tcos(
tcos(![]() . t). Vendar pa, ko je t = 0 dobimo preprosto v0 = v0 (cos 0 = 1 in e0 = 1). Torej sledi:
. t). Vendar pa, ko je t = 0 dobimo preprosto v0 = v0 (cos 0 = 1 in e0 = 1). Torej sledi:
Wk = ![]() m . v02
m . v02
0, 2J = m . v02/2 ...Masa uteži ostaja enaka...torej jo lahko črtamo. Ob črtanju mase moramo upoštevati, da se tudi enote krajšajo.Lahko jo tudi pustite, saj se v naslednji enačbi krajša.
v0 = 0, 63m/s
Potem pa izračunamo še za energijo po 5s. In uporabimo Wk = W2
Za nihajni čas, ki se ne spreminja ne glede na amplitudo odmika, pogojen je namreč le s težnim pospeškom in dolžino nihala(pri nitnem nihalu), vzamemo t0 = 5s.
W2 = ![]() m . v02
m . v02
W2 = ![]() m . v02 . e-2
m . v02 . e-2![]() t . cos2(
t . cos2(![]() t)
t)
0, 1J = (m . 0, 4m2/s2 . e-2![]() 5s . cos2((2
5s . cos2((2![]() . 5s)/(5s)))/2 ...Maso ponovno črtamo. cos pa je enak ena, saj vemo da je periodičen na 2
. 5s)/(5s)))/2 ...Maso ponovno črtamo. cos pa je enak ena, saj vemo da je periodičen na 2![]() .
.
0, 5s = e-![]() 10s ...Za tiste , ki jim logaritmi niso povsem jasni.
10s ...Za tiste , ki jim logaritmi niso povsem jasni.
0, 5s = e![]() . e-10
. e-10
ln e![]() = ln
= ln![]()
![]() = 9, 3E
= 9, 3E
Končno rezultat.
Pol je treba pa še narisat. Če slučajno bere to kdo, ki ima Derive ali kak programček za risanje grafov, bi ga prosil, da doda graf. Hvala!!!
hmmm...po moje je treba najprej popraviti rešitev!
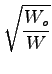
tako je
![]() = 0, 69s-1
= 0, 69s-1
x = xo/2
m . v2/2 = k . x2/2
m . vo2 . cos(![]() t) = k . xo2/4 = >
t) = k . xo2/4 = >
= > Wk = 4Wpr
hmmm...nekaj nagaja - gam neki je izginil člen
cos(![]() t)
t)
m . vo2 . cos(![]() t) = k . xo2/4
t) = k . xo2/4
ker je
vo2 = ![]() xo2 in
xo2 in
![]() = k/m
= k/m
vstavimo, pokrajšamo in ugotovimo, da je
cos(![]() t) = 1/4
t) = 1/4
medtem, ko enačba x = xo/2 pravi, da je
sin(![]() t) = 1/2
t) = 1/2
skratka pravilneje bi bilo:
m . vo2 . cos2(![]() t) = k . xo2/4
t) = k . xo2/4
...
=============================
glavna težava pa je v začetni preambuli Wk = Wpr, ker energiji nista enaki, ampak nas zanima, koliko je Wk/Wpr = ?
imamo dve možnosti:
1. začnemo z energijami: ker je
x = ![]() ali
ali
![]() =
= ![]() , mora biti razmerje med trenutno prožnostno energijo in skupno energijo (največjo prožnostno):
, mora biti razmerje med trenutno prožnostno energijo in skupno energijo (največjo prožnostno):
To pomeni, da je skupna energija 4 krat večja kot prožnostna.
Po drugi strani pa vemo, da je vsota kinetične in prožnostne energije v kateremkoli trenutku enaka skupni energiji. Z drugimi besedami: ker je Wk = Wo + Wpr, lahko sklepamo, da je razmerje med kinetično energijo in skupno energijo:
Tako ugotovimo, da je kinetična energija 3 krat večja, če je odmik enak polovici amplitude! Ali:
2. začnemo s podatkom
x = ![]()
ker mora hkrati veljati
x = xosin(![]() t) (če nihalo začnemo opazovati v ravnovesni legi), hitro izračunamo, da je
t) (če nihalo začnemo opazovati v ravnovesni legi), hitro izračunamo, da je
potem pogledamo, kako je z razmerjem kinetične in prožnostne energije v tem trenutku:
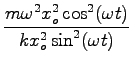 =
= 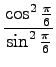 =
=
Wk = Wpr
m . v2/2 = k . x2/2
Uporabim enačbe za začetek nihanja v RL:
v = vocos(![]() . t)
. t)
x = xosin(![]() . t)
. t)
vem pa tudi da je:
vo = ![]() . xo
. xo
k(kg/s2) = > to = 2![]() . (m/k)1/2 =>
. (m/k)1/2 =>
=>
k = 4![]() . m/to2
. m/to2
sledi:
m . vo2 . cos2(![]() . t) = k . xo2 . sin2(
. t) = k . xo2 . sin2(![]() . t)
. t)
m . xo2 . ![]() . cos2(
. cos2(![]() . t) = k . xo2 . sin2(
. t) = k . xo2 . sin2(![]() . t)
. t)
m . ![]() /k = sin2(
/k = sin2(![]() . t)/cos2(
. t)/cos2(![]() . t)
. t)
m . (2![]() /to)2/4
/to)2/4![]() . m/to2 = tg2(
. m/to2 = tg2(![]() . t)
. t)
1 = tg(![]() . t) ...pazi ali računaš v radianih ali stopinjah
. t) ...pazi ali računaš v radianih ali stopinjah
pi/4 = (t . 2![]() )/to
)/to
t = to/8
oziroma kot ste lahko sklepali brez tega računa na polovici časa med RL in SL
x = xo . sin(![]() . t)
. t)
x = xo . sin((2![]() /to) . (to/8))
/to) . (to/8))
x = xo . sin(pi/4)
x = 0.87 . xo...ali...x = xo . 31/2/2
lahko bi poskusili tudi takole:
ker je: Wk = Wpr in je Wo = Wk + Wpr, sklepamo, da je:
Wo = 2Wpr, oziroma
če velja, da se odmik spreminja:
x = xosin(![]() . t)
. t)
potem se prožnostna energija spreminja:
zato je razmerje energij
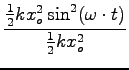
ali
korenimo:
negativne rešitve nas ne zanimajo, ker čas ne teče nazaj!
ostane nam
sin(![]() . t) =
. t) = ![]() =
= ![]()
oziroma
![]() . t =
. t = ![]()
ker je:
![]() =
= ![]()
poiščemo še čas:
mogoče malo krajše ali pa tudi ne ;)
me 2007-11-05