Naprej: geometrijska optika Navzgor: valovanje Nazaj: valovanje Kazalo
zrak n2 = 1 (isto kot v vakuumu)
![]() = 57o
= 57o
![]() =
= ![]()
![]() = arcsin(sin
= arcsin(sin![]() . n1)
. n1)
![]() = arcsin(sin(57 . 1.5)
= arcsin(sin(57 . 1.5)
![]() == hmm hecno ne gre ker je kot večji k 90 stopinj, oziroma arcsin x.. ko je x > 1 se ne da zračunati.
== hmm hecno ne gre ker je kot večji k 90 stopinj, oziroma arcsin x.. ko je x > 1 se ne da zračunati.
Iz tega lahko sklepamo da tukaj svetloba sploh ne pride iz stekla v zrak ampak se odbije nazaj. Zgodi se POPOLN ODBOJ!!!!
kot pod katerim se odbije nazaj:
57o
zrak n2 = 1 (isto kot v vakuumu)
![]() = 57o
= 57o
![]() = arcsin(sin
= arcsin(sin![]() . n1)
. n1)
![]() = arcsin(sin(57 . 1.3)
= arcsin(sin(57 . 1.3)
![]() = = hmm hecno ne gre ker je kot večji k 90 stopinj, oziroma arcsin x .. ko je x > 1 se ne da zračunati.
= = hmm hecno ne gre ker je kot večji k 90 stopinj, oziroma arcsin x .. ko je x > 1 se ne da zračunati.
Torej se svetloba odbije nazaj v vodo, pod istim kotom kot je zadela vodno gladino. Zgodi se POPOLN ODBOJ.
n1 = 1 (zrak)
n2 = 1, 5 (odvisno od tipa stekla)
![]() = 55o
= 55o
![]() =
= ![]()
![]() = arcsin(sin
= arcsin(sin![]() .
. ![]() )
)
![]() = arcsin(sin(57/1.5)
= arcsin(sin(57/1.5)
![]() = 33o
= 33o
Pazi! Kot ![]() mora biti manjši od alfa ko gre žarek iz optično redkejše v optično gostejšo snov.
mora biti manjši od alfa ko gre žarek iz optično redkejše v optično gostejšo snov.
n nam pove kolikokrat počasneje se širi svetloba v X snovi kot v zraku.
n1 = 1 (zrak)
n2 = 1.5 (steklo)
![]() = 30o
= 30o
![]() =
= ![]()
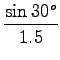
Potem pa še v olju:
(hmm hecno za zdej se ne vem lomnega količnika olja bom rešil ko ga dobim...lahko pa kdo drug nadaljuje. In my dreams!")
Vprašanje o zamaknjenosti snopa svetlobe je nekoliko dvoumno. Ni mi jasno, ali je potrebno izračunati, koliko je točka izstopa snopa iz stekla premaknjena glede na prvotno smer, kar sem označil z y, ali pa naj bi izračunal, koliko je lomnljeni snop premaknjen od prvotne smeri, kar sem označil z x. V prvem primeru je očitno:
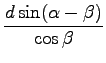 = 0, 892cm
= 0, 892cm
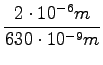 = 3, 17
= 3, 17
Pasovi oslabitve so med pasovi ojačitve. Torej jih je 8.
Smer=?
smer določiš s pogojem oslabitve:
d sin![]() =
= ![]() (2n - 1) in izračunaš kot
(2n - 1) in izračunaš kot ![]()
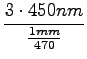 = 0, 63
= 0, 63
<a href="http://www2.arnes.si/~oskrzr2/Timko2002_03/Barve/ \ organska\%20barvila.htm">Tukaj najdete barve valovnih dol�in</a>poznam pogoj ojačenja: n
l1 = l2
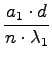 =
= 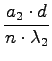
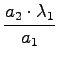 =
= 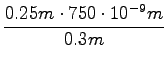 = 625nm
= 625nm
Barva je torej še vedno rdeča, vendar bolj živo rdeča.
me 2007-11-05