Naprej: moderna fizika Navzgor: elektrika Nazaj: magnetno polje Kazalo
Ui = ![]() . (
. (![]() ×
×![]() )
)
ter:
![]() = (Bx, 0, Bz),
= (Bx, 0, Bz),
![]() = (0, l, 0) in
= (0, l, 0) in
![]() = (v, 0, 0)
= (v, 0, 0)
sedaj izračunamo vektorski in skalarni produkt in dobimo:
Ui = vlBz =...V
F = Fm = IilB =...N
in pospešek:
ma = IilB =>
a = ![]() =...
=...![]()
Ui = ![]() . (
. (![]() ×
×![]() )
)
torej poznam tudi tole velikost:
Ui = v cos(![]() )lB sin(
)lB sin(![]() )
)
Ui![]() t =
t = ![]()
![]() = NBS = NB
= NBS = NB![]() r2...Vs
r2...Vs
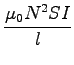 =...Vs
=...Vs
N1 = 100,
l1 = 0, 8m, r1 = 5cm, I1 = 2A, ter
N2 = 1000 in r2 = 3cm in
![]() = 30o
= 30o
a)
A = ![]() =
= 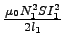 =...J
=...J
b)
![]() = L1I1 =...Vs
= L1I1 =...Vs
c)
Ui![]() t = N2B1S2cos
t = N2B1S2cos![]() =
= 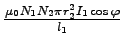 =...Vs
=...Vs
l1 = 0, 7m, N1 = 100,
![]() = 3
= 3![]() , N2 = 200 in r2 = 2cm
, N2 = 200 in r2 = 2cm
Ui = 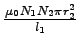
![]() =...V
=...V
Nt = 1000, rt = 10cm, lt = 50cm, lp = 10cm in It = 10A
Največja napetost ki se inducira je:
Ui = ![]() . (
. (![]() ×
×![]() ) = -
) = - ![]() lp2Bt
lp2Bt
vem pa tudi, da zaradi nihanja velja enačba:
M = - Jp![]()
=>
Fgr'sin![]() - Fmr' = - Jp
- Fmr' = - Jp![]()
če velja
sin![]() =
= ![]() ,
ap = - x
,
ap = - x![]() in
x = rt
in
x = rt
mpgr'![]() x - IilpBtr'2 = - Jpap
x - IilpBtr'2 = - Jpap
izpeljava je predolga, a ne prezapletena, rešitev:
![]() =
= ![]() -
- ![]()
=>
Ui2 = ![]() lp4Bt2
lp4Bt2
dobimo kvadratno enačbo in njeni rešitvi:
Ui1 = - ![]() +
+ 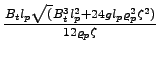
in
Ui1 = - ![]() -
- 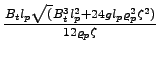
Fg = Fm
torej:
IiaB = 4![]() Sag
Sag
![]() B = 4Sg
B = 4Sg![]()
potem:
Bav = ![]()
=>
v = ![]()
me 2007-11-05