Naprej: pospešeno Navzgor: gibanje Nazaj: gibanje Kazalo
![]() = 7km/h
= 7km/h
![]() = 12km/h
= 12km/h
![]() = 15km/h
= 15km/h
![]() s1 = 21km
s1 = 21km
![]() s2 = 20km
s2 = 20km
![]() s3 = 18km
s3 = 18km
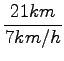 +
+ 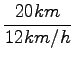 +
+ 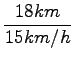
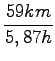
najprej se vprašajmo - koliko časa je vozil vlak?
čas vožnje dobimo, ko seštejemo čas vožnje pred polnočjo in tistega po polnoči:
ta čas pretvorimo v sekunde
ker je hitrost predvidoma stalna:
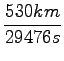 =
= 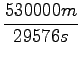 = 17, 9m/s = 64, 5km/h
= 17, 9m/s = 64, 5km/h
ker pripluje čoln iz A v B v 4h, razdalja med krajema pa je 24km, lahko izračunam hitrost čolna za opazovalca na bregu:
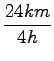 = 6km/h
= 6km/h
ker vozi čoln proti toku je hitrost reke:
nazaj grede pluje s tokom, torej je hitrost čolna za opazovalca na bregu večja:
zato je čas potovanja krajši:
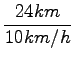 = 2, 4h = 2h24m
= 2, 4h = 2h24m
tako
v2 = 2m/s
v1 = ??? ...To je hitrost s katero zakotalimo kroglico po tekočem traku.
s = 10m
t = 2s
v1 = 3m/s...Kroglica se mora gibati 3m/s glede na trak.
Če jo zakotalimo v nasprotni smeri z isto hitrostjo se hitrost v1 in v2 odštejeta. Čas ostane 2s.
s1...Predstavlja pot, ki jo bo opravila kroglica če jo zakotalimo v nasprotno smer.
Kroglica se bo premikala v nasprotno smer od smeri gibanja tekočega traka, saj je njena hitrost večja od hitrosti traka.
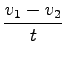
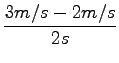
s1 = 0, 5m ...Samo toliko poti opravi, če jo zakotalimo v nasprotno smer.
s = 80km
v1 = 50km/h
v2 = 60km/h
ts = 10min = ![]() h...Čas za katerega se vstavi 2. avtomobil po 0, 5h.
h...Čas za katerega se vstavi 2. avtomobil po 0, 5h.
Čas, ki ga potrebuje 1. avtomobil do cilja:

Čas, ki ga potrebuje 2. avtomobil do cilja:
(Lahko ga izračunamo preprosto tako, da času, ki bi ga prevozil brez ustavljanja prištejemo 10 min.)
 +
+
Torej še vedno na cilj prispe drugi avto, katerega povprečna hitrost je bila 60km/h. Naj vas to ne zavede, po naseljih je še vedno omejitev 50km/h.
povprečna hitrost je definirana:
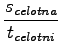
ker je žena vozila
![]() in prav toliko mož, lahko določimo časa, ki sta ga oba potrebovala za svojo polovico poti:
in prav toliko mož, lahko določimo časa, ki sta ga oba potrebovala za svojo polovico poti:
sedaj pa še vse skupaj vstavimo v enačbo za hitrost:
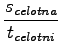 =
= 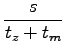 =
= 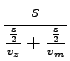
v imenovalcu izpostavimo s/2 pokrajšamo:
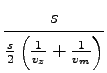
in dobimo:
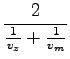 = 66, 7km/h
= 66, 7km/h
to kar smo dobili je pravzaprav harmonična sredina
kar seveda niti približno ni enako aritmetični sredini obeh hitrosti
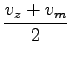 = 75km/h
= 75km/h
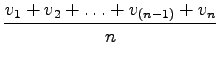
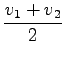
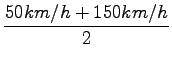
glej še prejšnjo nalogo: očitno je tako dobljena povprečna hitrost v nasprotju z definicijo poprečne hitrosti!
me 2007-11-05