Naprej: gibalna količina Navzgor: dinamika Nazaj: pri kroženju Kazalo
LUNA: r = 380000km
m = 7, 4 . 1022kg
ZEMLJA: M = 6 . 1024kg
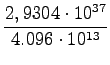
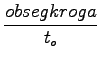 =
=
![$\displaystyle \sqrt[3]{{\left(\frac{t_o}{t_{oz}}\right)^2}}$](img137.gif) = 4, 95a.e.
= 4, 95a.e.
![$\displaystyle \sqrt[3]{{\left(\frac{11let}{1leto}\right)^2}}$](img138.gif) = 4, 95a.e.
= 4, 95a.e.
![$\displaystyle \sqrt[3]{{\left(\frac{t_o}{t_{oz}}\right)^2}}$](img137.gif)
![$\displaystyle \sqrt[3]{{\left(\frac{89let}{1leto}\right)^2}}$](img139.gif) = 20a.e.
= 20a.e.
in ker je višina enaka dvema radijema zemlje h = ro in je torej razdalja od središča Zemlje r = 2ro
je potemtakem
Fg ![]()
![]()
in ker je višina enaka dvema radijema zemlje h = 2ro in je torej razdalja od središča Zemlje r = 3ro
je potemtakem
Fg = ![]() = 1, 11N
= 1, 11N
v = 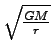 in odtod izrazimo r
in odtod izrazimo r
r = ![]() = 2, 5 . 107m = 25000km
= 2, 5 . 107m = 25000km
torej je višina h = r - ro = 18600km
v = 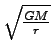 in odtod izrazimo r
in odtod izrazimo r
r = ![]() = 1 . 108m = 100000km
= 1 . 108m = 100000km
torej je višina h = r - ro = 93650km
me 2007-11-05