Naprej: energijski zakon Navzgor: dinamika Nazaj: gravitacija Kazalo
![]()
![]() =
= ![]() ;
;
Naj bo:
m =masa človečka in M =masa čolnička, ter v1 = hitrost človečka;
![]() =
= ![]()
torej:
![]() = m .
= m . ![]() + M .
+ M . ![]() ;
;
izrazimo v2, rečemo, da ima vektor v1 pozitiven predznak, torej ima ![]() negativnega in se zategadelj giblje v nasprotni smeri :)
negativnega in se zategadelj giblje v nasprotni smeri :)
![]()
![]() =
= ![]() ;
;
iz tega sledi:
![]() =
= ![]()
torej lahko zapišem tudi brez vektorjev zaenkrat:
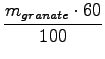 . v1 +
. v1 + 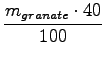 . v2;
. v2;
iz te enačbe lahko izrazim v2, zaenkrat pa računam samo velikost:
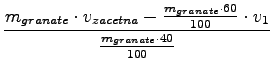 = - 12, 5m/s;
= - 12, 5m/s;
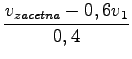
vem tudi da je smer vektorja ![]() nasprotno enaka smeri vektorja
nasprotno enaka smeri vektorja ![]() , ker ima v2 negativen predznak, privzeli pa smo, da ima začetna hitrost
, ker ima v2 negativen predznak, privzeli pa smo, da ima začetna hitrost
![]() pozitiven predznak;
pozitiven predznak;
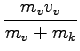 = 15m/s
= 15m/s
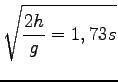
Skupna gibalna količina obeh drsalcev se pri takšnem odrivu ohrani, tako da v smeri, ki je pravokotna na prvotno smer gibanja, skupna gibalna količina ostane 0, toliko kot je bila pred odrivom. V smeri gibanja drsalcev pa gibalna količina tudi ostane tolikšna kot je bila prej, saj ni nobene zunanje sile, ki bi skupno gibalno količino spremenila.
V smeri, ki je pravokotna na prvotno smer gibnja obeh drsalcev lahko zapišemo izrek o ohranitvi gibalne količine:
![]() G = 0 ali
m1v1 = m2v2. Pri tem upoštevamo še, da je hitrost s katero se drsalca oddaljujeta drug od drugega enaka vsoti hitrosti posameznega drsalca v = v1 + v2. Eno hitrost izrazimo z drugo in vstavimo v izrek o ihranitvi gibalne količine. Po krajšem računu, ki ga naj bralec za vajo naredi sam, ugotovimo, koliko sta hitrosti drsalcev v smeri, ki je pravokotna na prvotno smer gibanja:
G = 0 ali
m1v1 = m2v2. Pri tem upoštevamo še, da je hitrost s katero se drsalca oddaljujeta drug od drugega enaka vsoti hitrosti posameznega drsalca v = v1 + v2. Eno hitrost izrazimo z drugo in vstavimo v izrek o ihranitvi gibalne količine. Po krajšem računu, ki ga naj bralec za vajo naredi sam, ugotovimo, koliko sta hitrosti drsalcev v smeri, ki je pravokotna na prvotno smer gibanja:
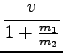 = 1, 09m/s in v2 =
= 1, 09m/s in v2 = 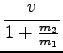 = 1, 91m/s
= 1, 91m/s
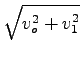 = 4, 15m/s in vd =
= 4, 15m/s in vd = 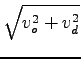 = 4, 43m/s
= 4, 43m/s
![]()
![]() =
= ![]() -
- ![]()
![]()
![]() G = 2G2cos
G = 2G2cos![]() = 17, 3Ns,
= 17, 3Ns,
F![]() t =
t = ![]() G = 17, 3Ns,
F =
G = 17, 3Ns,
F = ![]() = 173N, kot med smerjo sile in steno je 90o.
= 173N, kot med smerjo sile in steno je 90o.
t = ![]() = 6, 67s in zato
F =
= 6, 67s in zato
F = ![]() = 2, 25N
= 2, 25N
Ft = Fg![]() - F = 3, 75N
- F = 3, 75N
t = 3, 2s in zato F = 7, 81N
Ft = 4, 69N
me 2007-11-05