Naprej: hidrodinamika Navzgor: toplota Nazaj: tlak Kazalo
glej tudi nalogo 4(??) iz hidrodinamike!
koliko je tlak 10m pod gladino?(v Pa)
p = p0 + ![]() gh = 100000N/m2 +100000N/m2 = 200000Pa
gh = 100000N/m2 +100000N/m2 = 200000Pa
ko se dvigne tik pod gladino, se tlak zmanjša na zračni tlak p0, zato se prostornina poveča na V0 po Boylovem zakonu:
p0V0 = pV
upoštevam še povezavo
V = ![]()
![]() r3
r3
izrazim r0:
Sedaj lahko izračunamo sili:
Fg = mg = 100![]() N,
Fv =
N,
Fv = ![]() Vg = 51, 4
Vg = 51, 4![]() N torej je razlika velikosti sil (rezultanta!=):
Fg - Fv = 48, 6
N torej je razlika velikosti sil (rezultanta!=):
Fg - Fv = 48, 6![]() N in končno pospešek:
N in končno pospešek:
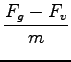 = 4, 86m/s2
= 4, 86m/s2
Pri računanju največje hitrosti moramo upoštevati še silo upora na žogico. Kadar je hitrost žogice največja, mora biti rezultanta sil enaka nič, ali drugače
Fg - Fv - Fu = 0. Ker je sila upora
Fu = Fg - Fv = 48, 6![]() N, lahko izračunamo hitrost (upoštevamo kvadratni zakon upora, čeprav še ne vemo, ali je to upravičeno)
N, lahko izračunamo hitrost (upoštevamo kvadratni zakon upora, čeprav še ne vemo, ali je to upravičeno)
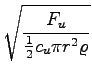 = 0, 745m/s
= 0, 745m/s
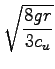
![$\displaystyle \sqrt[3]{{\frac{3V}{4\pi}}}$](img205.gif) = 1, 34mm
= 1, 34mm
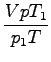 = 19, 2mm3
= 19, 2mm3
![$\displaystyle \sqrt[3]{{\frac{3V_1}{4\pi}}}$](img208.gif) = 1, 66mm
= 1, 66mm
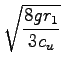 = 0, 3
= 0, 3
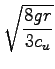
![$\displaystyle \sqrt[3]{{\frac{3V}{4\pi}}}$](img205.gif) = 1, 68mm
= 1, 68mm
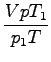 = 57, 7mm3
= 57, 7mm3
![$\displaystyle \sqrt[3]{{\frac{3V_1}{4\pi}}}$](img208.gif) = 3, 86
= 3, 86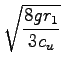 = 0, 45
= 0, 45
me 2007-11-05