hidrodinamika

1. Voda odteka s strehe po navpičnem žlebu z dolžino 10m. Kako daleč od vznožja stavbe moramo v tla izkopati odtočni jašek, če je iztočna šoba žleba vodoravna in 20cm nad tlemi?

   Rp:

   najprej izračunamo s kakšno hitrostjo odteka voda iz žleba:

   v = $\sqrt{{2gh_1}}$ = 14m/s

   ; kjer je h₁ = 10m, g = 10m/s²

   sedaj imamo en čist navaden poševni met :)

   h₂ = 20cm

   vem:

   h₂ = $${\frac{{1}}{{2}}}$$g ^. (t²)

   s = v ^. t.

   t iz prve enačbe vstavim v drugo in dobim:

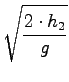   s = v ^. $$\sqrt{{\frac{2\cdot h_2}{g}}}$$ = 2, 8m

2. Sod ima na višini 0, 5m od tal odprtino za točenje vina. Na kolikšni razdalji od vznožja soda moramo postaviti na tla kozarec, da curek prestrežemo? Sod je visok 1, 2m in do vrha poln.

   Rp:

   najprej lahko zracunam hitrost iztekanja vode :)

   v = $\sqrt{{2gh_1}}$ = 4.9m/s) in g = 10m/s² ter h₁ = 1.2m

   nato izracunam cas padanja:

   t = $\sqrt{{\frac{2h_2}{g}}}$

   kjer je h₂ = 0.5m

   in sedaj:

   s = v ^. t = 1.5m

3. Iz 5m visokega plavža izlivajo talino v kalup. Kako daleč od iztočne šobe, ki je 0, 5m nad tlemi, naj kalup namestijo?

4. V vodi s temperaturo 20^oC se dviga zračni mehurček s hitrostjo 5mm/s. Kolikšen je premer mehurčka?

   Rp:

   vem: na mehurcek delujejo tele sile:

   $\vec{F}_{g}^{}$ + $\vec{F}_{{u}}^{}$ + $\vec{F}_{{vzg}}^{}$ = $\vec{0}$;

   vem tudi tole:

   F_g + F_u = F_vzg;

   iz tega sledi enacba (F_g sem kar zanemaril, c_u = 1, 1 za kroglo):

   $${\frac{{1}}{{2}}}$$ ^. c_u ^. $$\varrho_{v}^{}$$ ^. S ^. v² = $$\varrho_{v}^{}$$ ^. g ^. V_izp;

   sedaj pa se spomnim tudi tole, ker pri urah matematike ne spim,kajne:

   V_izp = ${\frac{{4}}{{3}}}$ ^. S ^. r;

   sem zelo vesel, ker se mi nekatere stvari lepo pokrajßajo. In dobim enačbo za S, ki je enak $\pi$r². Sedaj imam:

   S = $$\pi$$$$\left(\vphantom{\frac{3}{8}\frac{c_u\cdot v^2}{g}}\right.$$$${\frac{{3}}{{8}}}$$$${\frac{{c_u\cdot v^2}}{{g}}}$$$$\left.\vphantom{\frac{3}{8}\frac{c_u\cdot v^2}{g}}\right)^{2}_{}$$ = 3, 5 ^. 10^-6mm²;

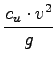
   ßal smo zelo zacudeni, ker nam ni bilo potrebno upoštevati T vode.

   glej še orehe!

   še o radiju:

   če ne upoštevamo teže:

   r = $${\frac{{3}}{{8}}}$$$${\frac{{c_u\cdot v^2}}{{g}}}$$

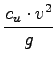
   če upoštevamo težo:

   r = $${\frac{{3}}{{8}}}$$$${\frac{{c_u\cdot v^2\varrho_v}}{{g (\varrho_v - \varrho_m)}}}$$

5. Kolikšen premer imajo kapljice dežja, ki padajo s hitrostjo 9m/s?

6. Kako velik premer mora imeti padalo, da pada 800N težak padalec s hitrostjo 5m/s? Koeficient upora je 1,3.

7. S kolikšno hitrostjo začne teči zrak v posodo, iz katere je zrak popolnoma izsesan?
8. Po cevi s polmerom 10cm teče voda s hitrostjo 1m/s. Cev se zoži, tako da je hitrost vode v njej 3m/s. Kolikšen je nov polmer cevi?

9. S kolikšno stalno hitrostjo pada v vodi kroglica z maso 0, 01kg in polmerom 1cm? Koeficient upora krogle je c = 0, 4.

10. Kolikšno silo mora v vodoravni smeri prenesti podporni steber mostu, če stoji sredi reke, ki teče s hitrostjo 8m/s? Steber je širok 0, 5m, voda pa globoka 60cm.

11. Kako je polmer mehurčka zraka v vodi odvisen od globine, kjer se nahaja? Kako se mehurček giblje? Kako se spreminjata hitrost in pot v odvisnosti od časa?

    Rp:

    problem zastavimo v dveh večjih korakih

    Slika 24: sile na mehurček zraka v vodi

    

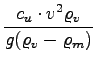
    najprej statično, nato dinamično

    pri statičnem reševanju je vsota zunanjih sil enaka nič, pri dinamičnem pa ma

    statični približek uporabimo z izgovorom, da je sila vzgona nekaj 100 krat večja od teže, torej je pospešek tako velik, da mehurček v zelo kratkem času doseže svojo maximalno hitrost

    Glej slike 38 in rešitev na !

12. Obe nosnici skupaj imata presek 2cm². Kolikšna je hitrost zraka v nosnicah, kadar gre skoznje 0, 5l zraka na sekundo?

13. S kolikšno razliko tlakov lahko damo zraku hitrost 10m/s?

14. Iz enakih posod z enakimi luknjicami iztekata zrak in helij pod enakima tlakoma. Kateri plin izteka hitreje in kolikokrat hitreje, če je gostota zraka 7, 25× tolikšna kot gostota helija?

15. Kolikšno največjo hitrost doseže pri padanju v zraku gumijasta žoga s premerom 20cm? [ $\varrho_{{zrak}}^{}$ = 1, 2kg/m³, $\varrho_{{zoga}}^{}$ = 7, 8kg/m³]

16. Kako hitro se dviguje balon premera 2m napolnjen s helijem, ki nosi breme 1kg? Plašč balona tehta 250g. [ $\varrho_{{zrak}}^{}$ = 1, 29kg/m³, $\varrho_{{He}}^{}$ = 0, 178kg/m³, $\eta_{{zrak}}^{}$ = 1, 7 ^. 10^-5kg/sm = 1, 7 ^. 10^-5Ns/m², c_u = 0, 4kg/m³]

17. Kolikšen upor deluje na kroglast kamen s premerom 2cm, če leti po zraku s hitrostjo 10m/s? Ali smemo ta upor v primeri s težo kamna zanemariti, če računamo na 5% natančno? [ $\varrho_{{zrak}}^{}$ = 1, 2kg/m³, $\varrho_{{zoga}}^{}$ = 2, 7kg/m³]

18. Sava pri Šmartnem pri Ljubljani je poleti široka 50m in povprečno 1m globoka ter nosi 50m³ vode na sekundo. Kolikšna je povprečna hitrost vode?

19. S kolikšno največjo hitrostjo lahko brizga voda iz počene vodovodne cevi, v kateri je tlak za 3 bare večji kot zunaj?

20. Iz enakih posod z enakimi luknjicami iztekata zrak in vodik pod enakima tlakoma. Kateri plin izteka hitreje in kolikokrat hitreje, če je gostota zraka 14, 4× tolikšna kot gostota vodika?

21. Kolikšno največjo hitrost doseže pri padanju v zraku jeklena kroglica s premerom 2mm? [ $\varrho_{{zrak}}^{}$ = 1, 2kg/m³, $\varrho_{{jekla}}^{}$ = 7, 8kg/m³]

22. V vodi spustimo kovinsko kroglico s premerom 2cm, da pada proti dnu. Merimo hitrost kroglice v odvisnosti od časa. Podatki so podani v tabeli:

    t[s]	0	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9	1,0
    v[m/s]	0	0,73	1,23	1,45	1,58	1,60	1,61	1,62	1,63	1,63	1,63

    Nariši graf hitrosti v odvisnosti od časa in na njem določi največjo hitrost, ki jo doseže kroglica! Koliko je masa kroglice, če je koeficient upora 0, 4?

    Rp:

    Točke hitro vnesemo v graf in jih povežemo z gladko krivuljo, ki se jim kar najbolje prilega (slika 25). Največjo hitrost lahko določimo grafično: to je tam, kjer je krivulja vodoravna; ali pa iz tabele, saj se vrednosti za hitrost pri zadnjih treh časih ponovijo.

    Slika 25: Graf hitrosti v odvisnosti od časa za gibanje telesa, kadar moramo upoštevati upor sredstva, skozi katerega se giblje predmet.

    

    Maso kroglice izračunamo s pomočjo največje hitrosti. Kadar se hitrost telesa ne povečuje več, potem je sila upora na telo nasprotno enaka vsoti ostalih sil, ki delujejo na telo. V našem primeru, vleče teža kroglico navzdol, vzgon pa navzgor. Razlika teže in vzgona je zato enaka sili upora. Tako izrazimo težo, izraz poenostavimo in izračunamo:

    F_g = F_v + F_u = $$\varrho$$$$\pi$$r²$$\left(\vphantom{\frac{4}{3}r g + \frac{1}{2} c_u v^2}\right.$$$${\frac{{4}}{{3}}}$$rg + $${\frac{{1}}{{2}}}$$c_uv²$$\left.\vphantom{\frac{4}{3}r g + \frac{1}{2} c_u v^2}\right)$$ = 0, 209N

    Tako ugotovimo, da je masa kroglice 21g.

    Nekateri radi veliko računajo in si sproti zapisujejo vmesne rezultate. V našem primeru bi najprej izračunali prostornino V = ${\frac{{4}}{{3}}}$$\pi$r³ = 4, 19cm³, potem silo vzgona F_v = 0, 0419N in silo upora F_u = 0, 167N. Njuna vsota je enaka teži kroglice F_g = F_v + F_u = 0, 209N in tako je masa m = 20, 9g.

23. Z dna globokega bazena spustimo leseno kroglico s premerom 2dm, da se dviguje proti površju. Merimo hitrost kroglice v odvisnosti od časa. Podatki so podani v tabeli:

    t[s]	0	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9	1,0
    v[m/s]	0	0,76	1,27	1,54	1,64	1,70	1,71	1,72	1,73	1,73	1,73

    Nariši graf hitrosti v odvisnosti od časa in na njem določi največjo hitrost, ki jo doseže kroglica! Koliko je masa kroglice, če je koeficient upora 0, 4?

    Rp:

    V = ${\frac{{4}}{{3}}}$$\pi$r³ = 4, 19dm³, F_v = 41, 9N, F_u = 18, 8N, F_g = F_v - F_u = 23N, m = 2, 3kg.

24. Na enaki globini pod površino Bohinjskega jezera sta dva mehurčka, ki imata enako maso plina. V prvem mehurčku je ogljikov dioksid, v drugem pa vodik. Relativna atomska masa ogljika je 12, kisika 16 in vodika 1. Na gladini jezera je tlak 937 mbar, temperatura zraka in vode je povsod enaka 4^oC. Oba mehurčka sta dosegla največjo hitrost. Kateri mehurček se giblje z večjo hitrostjo? Koliko je razmerje med obema hitrostima dvigovanja?
    (*)Kako in zakaj se spremeni razmerje hitrosti mehurčkov, če se spremenita tlak in temperatura vode?

    Rp:

    Če predpostavimo, da je teža plina v mehurčku zanemarljiva glede na vzgon F_g $\ll$ F_v, potem lahko iz enakosti sile vzgona in sile upora F_v = F_u, na katero sklepamo iz stalne hitrosti mehurčka, izračunamo hitrost mehurčka ob pogoju, da je le-ta okrogel.

    $${\frac{{4}}{{3}}}$$$$\pi$$r³$$\varrho_{v}^{}$$g = $${\frac{{1}}{{2}}}$$c_u$$\pi$$r²$$\varrho_{v}^{}$$v²

    Ob dveh predpostavkah: teža je zanemarljiva in `mehurček je okrogel' (si se že kdaj potapljal?) ugotovimo:

    v² = $${\frac{{8gr}}{{3c_u}}}$$     $$\rightarrow$$     v $$\propto$$ $$\sqrt{{r}}$$

    Ker je po drugi strani tudi res r = ${\frac{{3V}}{{4\pi}}}$, torej r $\propto$ $\sqrt[3]{{V}}$, mora nujno biti ob naših prepostavkah res, da je v $\propto$ $\sqrt[6]{{V}}$. Tako dobimo za razmerje hitrosti v odvisnosti od prostornine:

    $${\frac{{v_1}}{{v_2}}}$$ = $$\sqrt{{\frac{r_1}{r_2}}}$$ = $$\sqrt[6]{{\frac{V_1}{V_2}}}$$

    Ko v enačbo vstavimo prostornino izraženo iz plinskega zakona V = ${\frac{{mRT}}{{Mp}}}$, se kopica količin pokrajša in dobimo:

    $${\frac{{v_1}}{{v_2}}}$$ = $$\sqrt[6]{{\frac{M_2}{M_1}}}$$ = 1, 67

    Ugotovimo lahko, da večja kot je molska masa plina, manjša je njegova hitrost.

    (*) se očitno ne spremeni

    Pretresimo predpostavke:

    če upoštevamo še težo plina v mehurčku:

    v² = $${\frac{{8gr}}{{3c_u}}}$$$$\left(\vphantom{1-\frac{\varrho_p}{\varrho_vv} }\right.$$1 - $${\frac{{\varrho_p}}{{\varrho_vv}}}$$$$\left.\vphantom{1-\frac{\varrho_p}{\varrho_vv} }\right)$$

    tako po krajšem računu ugotovimo:

    $${\frac{{v_1}}{{v_2}}}$$ = $$\sqrt[6]{{\frac{M_2}{M_1}}}$$$$\sqrt{{\frac{1-aM_1}{1-aM_2}}}$$

    kjer je a odvisen od tlaka in temperature:

    a = $${\frac{{p}}{{\varrho_v R T}}}$$ $$\simeq$$ 8, 59 ^. 10^-5$${\frac{{kmol}}{{kg}}}$$

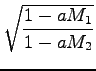
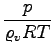
    Nisem še uspel razrešiti problem oblike mehurčka.

25. Na enaki globini pod površino Blejskega jezera sta dva mehurčka, ki imata enako maso plina. V prvem mehurčku je didušikov monoksid (smejalni plin), v drugem pa vodik. Relativna atomska masa kisika je 16, dušika 14 in vodika 1. Na gladini jezera je tlak 943 mbar, temperatura zraka in vode je povsod enaka 7^oC. Oba mehurčka sta dosegla največjo hitrost. Kateri mehurček se giblje z večjo hitrostjo? Koliko je razmerje med obema hitrostima dvigovanja?
    (*)Kako in zakaj se spremeni razmerje hitrosti mehurčkov, če se spremenita tlak in temperatura vode?

    Rp:

    $${\frac{{v_1}}{{v_2}}}$$ = $$\sqrt[6]{{\frac{M_2}{M_1}}}$$ = 1, 67