Naprej: energijski zakon Navzgor: toplota Nazaj: plinski zakon Kazalo
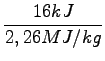 = 7g
= 7g
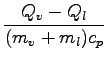 =
= 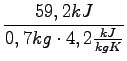 = 20, 1oC
= 20, 1oC
| t[s] | 0 | 20 | 40 | 60 | 80 | 100 | 120 | 140 | 160 | 180 |
| T[oC] | 63 | 51,7 | 46,9 | 44,0 | 42,5 | 41,4 | 40,7 | 39,7 | 39,5 | 39,5 |
Nariši graf temperature v odvisnosti od časa! Koliko je zmesna temperatura? Koliko vode je bilo na začetku v posodi?
![\includegraphics[width=180pt]{zmesna-temp}](img203.png)
|
Začetno maso vode lahko določimo, če predpostavimo, da je opazovani sistem zares toplotno izoliran. Pomeni, da led prejme natanko toliko toplote kot jo voda odda:
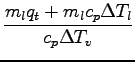 =
= 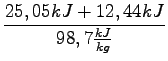 = 0, 3798kg = 380g
= 0, 3798kg = 380g
| t[s] | 0 | 20 | 40 | 60 | 80 | 100 | 120 | 140 | 160 | 180 |
| T[oC] | 48 | 36,7 | 31,9 | 29,0 | 27,5 | 26,4 | 25,7 | 24,7 | 24,6 | 24,6 |
Nariši graf temperature v odvisnosti od časa! Koliko je zmesna temperatura? Koliko ledu smo dodali v posodo?
me 2007-11-05