orehi

1. V vodi s temperaturo 20^oC se dviga zračni mehurček s hitrostjo 5mm/s. Kolikšen je premer mehurčka?

   Rp:

   vem: na mehurcek delujejo tele sile (glej še sliko 24 na strani ):

   $\vec{F}_{g}^{}$ + $\vec{F}_{{u}}^{}$ + $\vec{F}_{{vzg}}^{}$ = $\vec{0}$;

   vem tudi tole:

   F_g + F_u = F_vzg;

   iz tega sledi enacba (F_g sem kar zanemaril, c_u = 1, 1 za kroglo):

   $${\frac{{1}}{{2}}}$$ ^. c_u ^. $$\varrho_{v}^{}$$ ^. S ^. v² = $$\varrho_{v}^{}$$ ^. g ^. V_izp;

   sedaj pa se spomnim tudi tole, ker pri urah matematike ne spim,kajne:

   V_izp = ${\frac{{4}}{{3}}}$ ^. S ^. r;

   sem zelo vesel, ker se mi nekatere stvari lepo pokrajßajo. In dobim enačbo za S, ki je enak $\pi$r². Sedaj imam:

   S = $$\pi$$$$\left(\vphantom{\frac{3}{8}\frac{c_u\cdot v^2}{g}}\right.$$$${\frac{{3}}{{8}}}$$$${\frac{{c_u\cdot v^2}}{{g}}}$$$$\left.\vphantom{\frac{3}{8}\frac{c_u\cdot v^2}{g}}\right)^{2}_{}$$ = 3, 5 ^. 10^-6mm²;

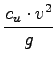
   ßal smo zelo zacudeni, ker nam ni bilo potrebno upoštevati T vode.

   to doseßemo tako, da upoßtevamo se F_g;

   kajti vem:

   F_g = m ^. g, kjer lahko m, dobim iz plinske enačbe:

   pV_izp = $${\frac{{m}}{{M}}}$$RT;

   kjer je p = $\varrho_{v}^{}$gh, kjer je h višina, ki se spreminja po času. "Ce je hitrost stalna ( v = const. = 5mm/s), potem velja zveza: h = v ^. t in zato p = $\varrho_{v}^{}$gvt;

   Z malo domißlije in racunanja preidejo zgornje enacbe v ustrezno obliko:

   F_g = mg = V_izpp$${\frac{{Mg}}{{RT}}}$$ = $${\frac{{4}}{{3}}}$$Sr ^. $$\varrho_{v}^{}$$vt ^. $${\frac{{Mg}}{{RT}}}$$;

   in ce to vstavimo v enacbo:

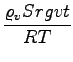   $${\frac{{4}}{{3}}}$$$${\frac{{\varrho_vSrgvt}}{{RT}}}$$M + $${\frac{{1}}{{2}}}$$ ^. c_u ^. $$\varrho_{v}^{}$$ ^. S ^. v² = $${\frac{{4}}{{3}}}$$$$\varrho_{v}^{}$$ ^. g ^. S ^. r;

   dobimo izredno presenetljivo:

   r(t) = $${\frac{{3}}{{8}}}$$$${\frac{{c_uRTv^2}}{{RT-Mvt}}}$$;

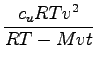   kar pomeni, da naß ljubi mehurcek spreminja obliko v odvisnost od casa, oziroma lege (h = vt);

   khm...pri tejle nalogi imam nekaj pomislekov

   Rezultat je sicer smiseln, ker radij mehurčka raste, ko čas teče. Ampak prav tako s časom narašča globina (??), tlak (??) in teža (????)

2. Kako je polmer mehurčka zraka v vodi odvisen od globine, kjer se nahaja? Kako se mehurček giblje? Kako se spreminjata hitrost in pot v odvisnosti od časa?

   Rp:

   problem zastavimo v dveh večjih korakih (glej še sliko 24 na strani )

   najprej statično, nato dinamično

   pri statičnem reševanju je vsota zunanjih sil enaka nič, pri dinamičnem pa ma

   statični približek uporabimo z izgovorom, da je sila vzgona nekaj 100 krat večja od teže, torej je pospešek tako velik, da mehurček v zelo kratkem času doseže svojo maximalno hitrost

   Slika 38: Gibanje mehurčka zraka v vodi I.

   [graf hitrosti v odvisnosti od globine (graf beremo od desne proti levi) bodi pozoren na merilo na ordinati, ki teče od 0.5m/s do 0.9m/s hitrost z manjšajočo se globino rahlo narašča - bliže ko je mehurček gladini, večjo hitrost ima]

   

   [graf hitrosti v odvisnosti od poti bodi pozoren na merilo na ordinati, ki teče od 0.5m/s do 0.9m/s hitrost rahlo narašča, ko se pot mehurčka veča]

   

   Slika 39: Gibanje mehurčka zraka v vodi II.

   [graf v(x) na celotni poti statično - zeleno dinamično - rdeče grafa se pokrivata]

   

   [graf v(x) na prvih nekaj desetink milimetra poti zeleno - statični približek rdeče - dinamični izračun lepo se vidi, kako se grafa hitro srečata]

   

   [graf x(t) na celotni poti zeleno - statični približek rdeče - dinamični izračun grafa sta praktično pokrita]

   

   [graf x(t) na prvih nekaj desetink milimetra poti zeleno - statični približek rdeče - dinamični izračun jasno je vidna razlika med obema pristopoma - vendar moramo upoštevati, da je to precej povečan pogled - vidimo zelo drobne podrobnosti, ki jih težko izmerimo]

   

   Slika 40: Gibanje mehurčka zraka v vodi III.

   [graf v(t) na celotni poti zeleno - statični približek rdeče - dinamični izračun]

   

   [graf v(t) na prvih nekaj desetink milimetra poti zeleno - statični približek rdeče - dinamični izračun]

   

   najprej statika:

   na mehurček delujejo sile (glej še sliko 24 na strani ):

   teža: F_g = mg = $\varrho_{z}^{}$Vg; kjer je $\varrho_{z}^{}$ je gostota zraka, prostornina mehurčka je V = ${\frac{{4}}{{3}}}$$\pi$r³

   vzgon: F_v = $\varrho_{v}^{}$Vg; kjer je $\varrho_{v}^{}$ je gostota vode, V je prostornina mehurčka

   sila upora: F_u = 1/2c_uS$\varrho_{v}^{}$v²; kjer je $\varrho_{v}^{}$ je gostota vode, presek mehurčka je S = $\pi$r²

   v ravnovesju velja: $\vec{{F}}_{v}^{}$ + $\vec{{F}}_{g}^{}$ + $\vec{{F}}_{u}^{}$ = 0

   oziroma (zapisano samo z velikostmi sil): F_v = F_g + F_u

   ker je gostota zraka $\varrho_{z}^{}$ okoli 1000 krat manjša od gostote vode, lahko silo teže zanemarimo! (v večjih globinah - pri večjih tlakih je razmerje med gostoto vode in gostoto zraka manjše in tam nekje pri globini 1000m ali več postaneta gostoti primerljivi)

   zato torej: F_v = F_u

   $\varrho_{v}^{}$Vg = 1/2c_uS$\varrho_{v}^{}$v², upoštevam pa še: V = ${\frac{{4}}{{3}}}$$\pi$r³ in S = $\pi$r²

   odtod dobim:

   r = $${\frac{{3 c_u v^2}}{{8 g}}}$$

   da je radij mehurčka sorazmeren s kvadratom hitrosti, oziroma, da je hitrost mehurčka sorazmerna s korenom iz radija:

   v = $$\sqrt{{\frac{8 g r}{3 c_u}}}$$

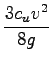
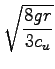
   tlak v vodi je odvisen od globine: p = p₀ + $\varrho_{v}^{}$gh

   prostornina mehurčka pa je odvisna od tlaka in temperature

   V = $${\frac{{m}}{{\varrho_z}}}$$ = $${\frac{{m R T}}{{p M}}}$$

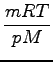
   R - splošna plinska konstanta, m - masa, M - molska masa, T - temperatura

   in tako je radij mehurčka:

   r = $$\sqrt[3]{{\frac{3V}{4\pi}}}$$ = $$\sqrt[3]{{\frac{3 m R T}{4\pi p M}}}$$

   mogoče je bolje meriti višino - to je pot, ne pa globine

   potem lahko odvisnost tlaka od poti x zapišem takole: p = p₀ + $\varrho_{v}^{}$g(h_z - x)

   najprej me zanima, kako je hitrost mehurčka odvisna od globine:

   v = $$\sqrt{{\frac{g}{c_u}}}$$$$\sqrt[6]{{\frac{2^7}{3^2\pi}}}$$$$\sqrt[6]{{\frac{mRT}{M}}}$$$$\sqrt[6]{{\frac{1}{p_0+g\varrho_vh}}}$$

   potem pa še odvisnost od poti:

   v = $$\sqrt{{\frac{g}{c_u}}}$$$$\sqrt[6]{{\frac{2^7}{3^2\pi}}}$$$$\sqrt[6]{{\frac{mRT}{M}}}$$$$\sqrt[6]{{\frac{1}{p_0+g\varrho_v(h_z-x)}}}$$

   ko hitrost kvadriramo dobimo še odvisnost radija od globine oziroma od poti odvisnost hitrosti od globine h oziroma od poti x si lahko ogledam tudi na grafu

   v obeh primerih je temperatura vode konstantna T = 27^oC

   na globini h = 10m je začetni polmer mehurčka r = 1cm

   oba grafa kažeta isto trditev, da hitrost mehurčka rahlo narašča, ko se mehurček bliža gladini

   težko pa v tem primeru kaj povemo o času dvigovanja mehurčka

   postopek presega običajno srednješolsko znanje matematike

   spomnimo se, da je hitrost definirana kot sprememba poti v časovni enoti:

   v = $${\frac{{\Delta x}}{{\Delta t}}}$$ = $${\frac{{dx}}{{dt}}}$$

   če je časovna enota dovolj majhna; enačbo malo obrnem:

   dt = $${\frac{{dx}}{{v}}}$$

   potem pa seštejem posamezne prispevke za čase od 0 do t in poti od 0 do x

   $$\int_{0}^{t}$$(dt) = $$\int_{0}^{x}$$$${\frac{{dx}}{{v}}}$$ =

   = $$\int_{0}^{x}$$$${\frac{{dx}}{{\sqrt{\frac{g}{c_u}}\sqrt[6]{\frac{2^7}{3^2\pi}}\sqrt[6]{\frac{mRT}{M}}\sqrt[6]{\frac{1}{p_0+g\varrho_v(h_z-x)}}}}}$$

   ko seštejemo, dobimo:

   t = $${\frac{{6(p_0 + g h_z\varrho_v)^{\frac{7}{6}}}}{{7 g \varrho_v \sqrt{\frac{g}{c_u}}\sqrt[6]{\frac{2^7}{3^2\pi}}\sqrt[6]{\frac{mRT}{M}}}}}$$$$\left(\vphantom{1-\left(1-\frac{g \varrho_v x}{p_0 - g \varrho_v h_z}\right)^{\frac{7}{6}}}\right.$$1 - $$\left(\vphantom{1-\frac{g \varrho_v x}{p_0 - g \varrho_v h_z}}\right.$$1 - $${\frac{{g \varrho_v x}}{{p_0 - g \varrho_v h_z}}}$$$$\left.\vphantom{1-\frac{g \varrho_v x}{p_0 - g \varrho_v h_z}}\right)^{{\frac{7}{6}}}_{}$$$$\left.\vphantom{1-\left(1-\frac{g \varrho_v x}{p_0 - g \varrho_v h_z}\right)^{\frac{7}{6}}}\right)$$

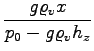
   pri izbranih začetnih podatkih (h_z = 10m, T = 27^oC) dobimo, da se mehurček zraka dviguje t = 12, 9605s (če sploh lahko merimo tako natančno)

   iz te enačbe lahko izpeljemo še, kako sta pot x in hitrost v odvisna od časa!

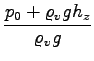
   x = $${\frac{{p_0+\varrho_v g h_z}}{{\varrho_v g}}}$$$$\left(\vphantom{1-\left(1-\frac{7 \varrho_v g \sqrt{\frac{g}{c_u}... ...RT}{M}}} {6(p_0 + g h_z\varrho_v)^{\frac{7}{6}}} t\right)^{\frac{6}{7}}}\right.$$1 - $$\left(\vphantom{1-\frac{7 \varrho_v g \sqrt{\frac{g}{c_u}}\sqrt[6... ...\pi}}\sqrt[6]{\frac{mRT}{M}}} {6(p_0 + g h_z\varrho_v)^{\frac{7}{6}}} t}\right.$$1 - $${\frac{{7 \varrho_v g \sqrt{\frac{g}{c_u}}\sqrt[6]{\frac{2^7}{3^2\pi}}\sqrt[6]{\frac{mRT}{M}}}}{{6(p_0 + g h_z\varrho_v)^{\frac{7}{6}}}}}$$t$$\left.\vphantom{1-\frac{7 \varrho_v g \sqrt{\frac{g}{c_u}}\sqrt[6... ...{mRT}{M}}} {6(p_0 + g h_z\varrho_v)^{\frac{7}{6}}} t}\right)^{{\frac{6}{7}}}_{}$$$$\left.\vphantom{1-\left(1-\frac{7 \varrho_v g \sqrt{\frac{g}{c_u}... ...RT}{M}}} {6(p_0 + g h_z\varrho_v)^{\frac{7}{6}}} t\right)^{\frac{6}{7}}}\right)$$

   solata! dinamični pristop

   za začetek zapišem 2.Newtonov zakon:

   $\vec{{F}}_{v}^{}$ + $\vec{{F}}_{g}^{}$ + $\vec{{F}}_{u}^{}$ = m$\vec{{a}}$

   z istim argumentom kot prej zavržem silo teže in upoštevam smeri sil:

   ma = $\varrho_{v}^{}$Vg - ${\frac{{1}}{{2}}}$c_uS$\varrho_{v}^{}$v²

   temule se reče diferencialna enačba!

   ker je ne znam rešiti(help!), se zadovoljim z numerično rešitvijo, da lahko vsaj primerjam rezultate, ki sem jih dobil v statičnem približku

   za numerično reševanje uporabim čarovnalnik, ker le-ti znajo precej dobro računati

   numerično izračunan čas dvigovanja mehurčka: t = 12.9607s kar se v okviru natančnosti pri merjenju gotovo ujema s časom, ki ga dobimo pri statičnem približku.

   razlika je posledica pospeševanja mehurčka v začetnih trenutkih

   ker je čas pospeševanja zelo kratek, je tudi razlika med statičnim približkom in dinamičnimi vrednostmi precej majhna

   primerjave so zbrane v grafih!

   čarovnalnik mi je narisal grafe: x(t), v(x) in v(t)

   statični približek je narisan zeleno, numerične rešitve dinamičnih enačb pa rdeče

   vsak graf je narejen za dva primera - za celotno pot in še posebej za začetek gibanja mehurčka

   iz grafov lepo vidimo, da na celotni poti ni grafično vidne razlike med grafi dobljene na statični ali dinamični način

   na drugi trojici grafov lahko opazujemo spreminjanje v začetnih trenutkih, kjer se pokaže razlika med statičnim približkom in dinamično rešitvijo

   Reynoldsovo število

   uh...toliko računanja, pa se še nismo prepričali, ali sploh smemo uporabiti kvadratni zakon upora

   zato hitro izračunam Reynoldsovo število in če bo dovolj veliko, potem sem lahko zadovoljen

   Re = ${\frac{{2r v \varrho_v}}{{\eta}}}$ = 16000

   ni slabo, Reynoldsovo število je dovolj veliko

3. Kozarec ima zanemarljivo majhno maso, njegov premer je 3cm, njegova višina pa 15cm. Vanj natočimo 2dl vode. Do katere višine seže voda? Kozarec postavimo na deščico, ki je prevlečena s smirkovim papirjem. Koeficient trenja med deščico in kozarcem je 1, 2. Na enem koncu začnemo deščico dvigovati. Kaj se zgodi? (predlogi: kozarec zdrsne, se prekucne, voda se izlije...)

4. Kaj se prej zvrne na klancu: togo telo v obliki kvadra, ali kanta napolnjena z vodo, če ima voda v kanti v vodoravni legi enake dimenzije kot togo telo? Masa kante je zanemarljivo majhna.

5. Kako se giblje klasičnega Jo-Jo?

6. nova